If you were asked to multiply 24 x 36, how would you do it? No calculuator!
Most of us (parents) learned what we now call the traditional algorithm, as shown below.
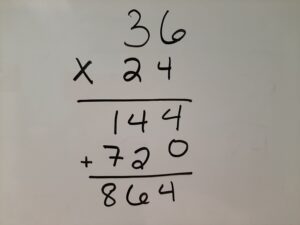
One technique that teachers have been demonstrating in the Common Core era is the box method for multiplication. At first, it seemed like too many steps but once I saw high schoolers using the method to expand polynomials, it all clicked! Fourth grade students in our county are taught the box method for multiplying two 2-digit numbers. By the time students reach Algebra 2 in high school, they are doing problems like my last example below… but the technique is the same!
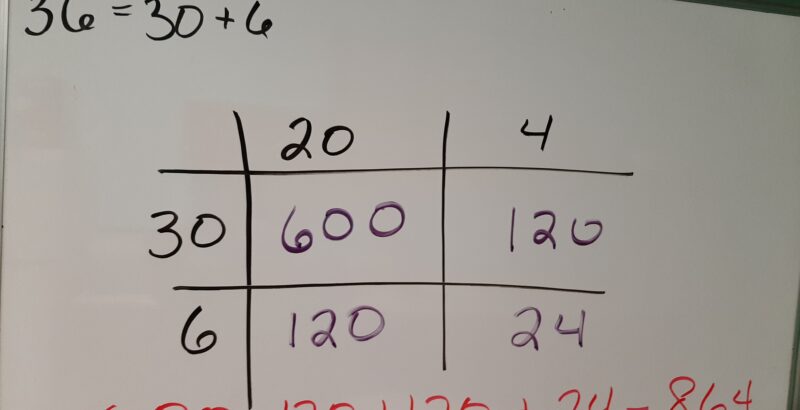
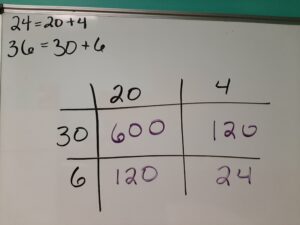
First, I will demonstrate our example 24 x 36 using the box method and then I will use the same method to multiply two linear binomials. To begin, separate your numbers by place value. The number 24 is made of two 10s (20) and four units (4). The number 36 is made of three 10s (30) and six units (6).

The numbers are split up into tens and ones
Then multiply the numbers in the grid.
The numbers inside the grid represents the products from multiplying the row by the column.
Finally, add all the numbers in the grid and that’s the answer!
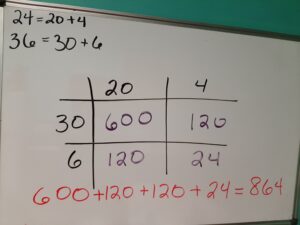
Now we’re just adding up all the products. Voila!
We can extend this lesson by thinking of polynomial multiplication. Below is an example that many of us learned using the FOIL method (first, outside, inside, last) but the box method works here too.
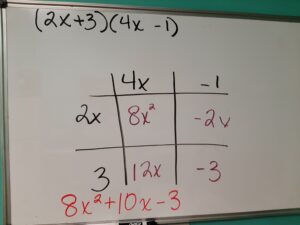
We can use the box method to find the product of two linear binomials.
Want to really go bananas with the box method? Check out this monster problem made much, much easier with this technique! For a little bonus math, notice that the like terms are diagonal from each other!
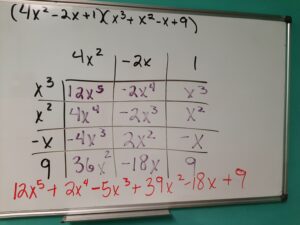
This problem shows the product of two big polynomials using the same method learned in 4th grade!